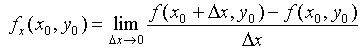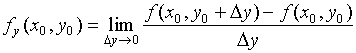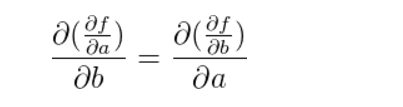偏导数

1.概念：

　　　　导数定义： 导数代表了在自变量变化趋于无穷小的时候，函数值的变化与自变量的变化的比值。几何意义是这个点的切线。物理意义是该时刻的（瞬时）变化率

　　　　注意：在一元函数中，只有一个自变量变动，也就是说只存在一个方向的变化率，这也就是为什么一元函数没有偏导数的原因。 

　　　　（derivative）

 

　　　　在中，一个多变量的函数的偏导数是它关于其中一个变量的，而保持其他变量恒定（相对于，在其中所有变量都允许变化）。

　　　　偏导数在和，以及中是很有用的。　　--引用自维基百科

　　　　　　

              

　　　　既然谈到偏导数，那就至少涉及到两个自变量。以两个自变量为例，z=f（x,y），从导数到偏导数，也就是从曲线来到了曲面。曲线上的一点，其切线只有一条。但是曲面上的一点，切线有无                  数条。而偏导数就是指多元函数沿着坐标轴的变化率。

               注意：直观地说，偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。

             （partial derivative）

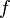
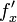
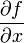
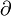
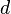
　　　　数学表示：函数关于变量x的偏导数写为或。偏导数符号是圆体字母，区别于全导数符号的正体。

　　　　由定义可求得：

                                 

                                  

　　　　

 　　　　偏导数对称性